GAZEUX (ÉTAT)

GAZEUX (ÉTAT)

La matière se présente sous quatre états (solide, liquide, gazeux, plasma), dont les propriétés sont très différentes. Pour un corps pur et sous une pression donnée, le passage de l’un de ces états à un autre se produit lorsque la température franchit certaines valeurs caractéristiques.

L’état gazeux présente, du point de vue macroscopique, trois propriétés principales:

– c’est un état de faible densité (la masse volumique de l’air, dans les conditions normales de température et de pression, est de 1,293 kg 練 m^-3);

– c’est un état où la matière est fortement compressible ; on constate en effet que le volume occupé par une certaine masse de gaz est a priori indéterminé; il dépend seulement des dimensions du récipient dans lequel le gaz est enfermé;

– enfin, cet état ne permet pas la conduction de l’électricité ; soumis à un champ électrique faible, un gaz pur est un isolant parfait .

La description «microscopique» de l’état gazeux fournit l’explication de ces diverses propriétés.

Un gaz est constitué de molécules (ou d’atomes dans le cas des gaz monoatomiques tels que les gaz rares) séparées par de grands espaces vides, ce qui explique la faible densité des gaz et leur forte compressibilité: les molécules occupent un volume de l’ordre du millième de celui qui leur est offert et la masse volumique d’un gaz est donc environ mille fois plus petite que celle de la matière condensée (solides ou liquides), dans laquelle les molécules sont en contact. Comprimer ou dilater un gaz revient simplement à faire varier le volume vide situé entre les molécules.

Le caractère d’isolant électrique tient au fait qu’un gaz ne contient aucune particule chargée libre (électrons ou ions positifs), mais seulement des molécules neutres. Des électrons libres et des ions positifs peuvent cependant apparaître si l’on soumet le gaz à un champ électrique de forte densité (décharge électrique dans les gaz) ou encore si on le chauffe à des températures suffisamment élevées (ionisation thermique). Lorsque l’ionisation est assez importante pour que le nombre d’électrons par unité de volume soit comparable à celui des molécules neutres, le gaz, devenu plasma, est un fluide très conducteur ^{[cf. PLASMAS]}.

Les molécules d’un gaz sont en perpétuelle agitation. Chacune d’elles suit une trajectoire en forme de ligne brisée constituée par des segments de droite reliés entre eux par des coudes brusques dus aux collisions entre deux molécules (cf. théorie CINÉTIQUE DES FLUIDES). Ce mouvement désordonné est appelé agitation thermique parce que l’énergie cinétique moyenne d’une molécule pour un gaz en équilibre thermodynamique est proportionnelle à la température absolue.

L’énergie interne d’un gaz comprend donc tout d’abord un terme qui est la somme des énergies cinétiques de translation des particules libres (atomes ou molécules) qu’il contient. Il peut s’y ajouter une certaine énergie d’excitation (rotation, vibrations, excitations électroniques) de ces atomes ou molécules, et une énergie de liaison constituée par la somme des énergies d’interaction entre les particules.

Lorsque ces énergies d’interaction sont négligeables, on introduit le concept de gaz parfait , fluide idéal, pour lequel l’énergie interne se réduit aux termes d’agitation thermique et d’excitation. Le gaz parfait correspond à un état limite dont s’approche tout gaz lorsque sa densité tend vers zéro: ses propriétés sont particulièrement simples et constituent une première approximation pour l’étude des gaz réels , dont les énergies d’interaction, quoique faibles, produisent des effets mesurables.

L’état gazeux est, parmi les états de la matière, celui qui, par sa nature même, est le plus simple à étudier; les propriétés d’un gaz se déduisent en effet directement de celles des molécules qui le constituent. De ce fait, la physique des gaz a joué, surtout entre 1870 et 1930, un rôle fondamental dans le développement de la théorie atomique et des méthodes de la mécanique statistique.

1. Description générale

Pour tout corps pur, on peut définir trois températures de changement d’état: la température de fusion-solidification (solide 燎 liquide) T^s ; la température de vaporisation-liquéfaction (liquide 燎 gaz) ^v; la température d’ionisation (gaz 燎 plasma) T^p .

Les températures de changement d’état varient avec la pression ; il est donc commode de faire apparaître sur un diagramme de coordonnées (T, P) le domaine occupé par chaque état de la matière. La figure 1 représente ce diagramme pour l’hydrogène. L’état gazeux est intermédiaire entre l’état liquide et l’état plasma. La courbe de l’équilibre liquide-gaz s’arrête au point critique C de coordonnées T^c et P^c . Pour les pressions supérieures à la pression critique P^c il y a continuité entre l’état liquide et l’état gazeux. Aux pressions inférieures à la pression P^t du point triple T, on passe directement de l’état solide à l’état gazeux (sublimation). On peut enfin remarquer que le passage de l’état gazeux à l’état plasma est un phénomène progressif qui se produit sur un certain intervalle de température et sans changement de phase.

Les tableaux 1, 2, 3 fournissent des listes de corps simples ou composés que l’on rencontre fréquemment à l’état gazeux. Ces corps sont caractérisés par une valeur relativement faible de la température ^v sous P^s = 1 atmosphère normale = 101 325 Pa (ou de la température de sublimation T^s pour les corps qui se subliment à cette pression).

Les grandeurs qui permettent de décrire l’état d’une certaine masse de gaz sont tout d’abord les trois variables d’état : température absolue T, volume V, pression P, puis deux grandeurs vectorielles permettant de décrire un mouvement éventuel du fluide, la vitesse du fluide ぴ, et le vecteur flux de chaleur り.

Enfin, pour une description microscopique détaillée, il est nécessaire d’introduire la fonction f ( ゐ) de distribution des vitesses des molécules (cf. théorie CINÉTIQUE DES FLUIDES). On utilise également les grandeurs auxiliaires suivantes: nombre de molécules N contenues dans le volume considéré; nombre de molécules par unité de volume ou «densité» numérique n ; volume spécifique v (volume par unité de masse); masse spécifique 福 ( 福 = v^-1 = n M); on fait intervenir également les fonctions thermodynamiques classiques: l’entropie S, l’énergie interne U, l’énergie libre de Helmholtz F = U 漣 TS, le potentiel thermodynamique de Gibbs G = U + PV 漣 TS, l’enthalpie H = U + PV.

Toutes ces grandeurs se classent en deux groupes: celui des variables «extensives» (V, N, S, U, F, G, H) et celui des variables «intensives» (P, T, face="EU Arrow" ぴ, り, f ( ゐ), n , 福). Les variables intensives caractérisent l’état local d’un gaz indépendamment de l’extension prise par celui-ci. Si l’on considère au contraire un certain volume ou une certaine masse homogène de ce gaz, les grandeurs extensives sont des variables globales proportionnelles au volume ou à la masse de gaz considéré. Les variables extensives, pour une quantité de matière de masse unité, sont les valeurs spécifiques (volume spécifique, entropie spécifique...).

2. Gaz parfaits en équilibre thermodynamique

Lorsqu’on enferme une certaine masse de gaz dans une enceinte de température T constante et uniforme (thermostat), il s’établit au bout d’un certain temps un équilibre thermodynamique entre le gaz et l’enceinte. Cet équilibre possède les propriétés suivantes: c’est un état stationnaire (indépendant du temps); la fonction de distribution des vitesses est isotrope et maxwellienne (cf. théorie CINÉTIQUE DES FLUIDES); les vecteurs vitesse du fluide ぴ et flux de chaleur り sont nuls; enfin, il existe entre les trois variables P, V, T une relation f (P, V, T) = 0, appelée équation d’état.

Équation d’état

La notion de gaz parfait s’est dégagée des travaux de Robert Boyle (1662), Edme Mariotte (1676), Jacques Alexandre César Charles (1798), Louis-Joseph Gay-Lussac (1802), Amedeo Avogadro (1811). Si l’on utilise la température absolue T, on montre que l’équation d’état des gaz parfaits se met sous l’une des formes classiques équivalentes:

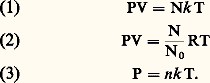On peut exprimer les constantes qui figurent dans ces diverses formules en utilisant la loi d’Avogadro: dans les conditions normales de pression et de température (P = P⁰, T = ⁰), le volume molaire V⁰ (volume occupé par une molécule-gramme c’est-à-dire par N = ⁰ molécules) est une constante universelle indépendante de la nature chimique du gaz. Dans ces mêmes conditions, la densité n ⁰ des molécules est également une constante universelle. Les valeurs numériques de V⁰, n ⁰ et ⁰ sont:

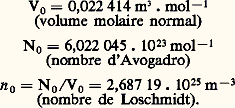On en déduit:

L’équation d’état (1) exprime les propriétés de dilatation thermique des gaz parfaits. On peut en effet en déduire la loi de dilatation à pression constante:

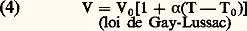et la loi d’augmentation de pression à volume constant:

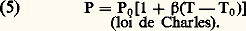Les deux coefficients 見 et 廓 sont d’ailleurs des constantes ( 見 est indépendant de P et 廓 indépendant de V) égales entre elles et universelles:

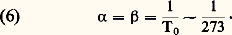L’ordre de grandeur de 見 montre enfin que les gaz sont environ mille fois plus dilatables que les solides usuels.

L’équation d’état (1) permet également de calculer le coefficient de compressibilité isotherme des gaz parfaits:

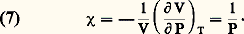Ce coefficient tend vers l’infini quand P tend vers zéro. À la pression atmosphérique, les gaz sont environ 10⁵ fois plus compressibles que les liquides usuels.

La représentation graphique de la loi des gaz parfaits peut se faire (fig. 2) sur un diagramme de coordonnées V, P (diagramme de Clapeyron) ou P, PV (diagramme d’Amagat). Sur le premier, les isothermes sont des hyperboles équilatères et sur le second, des droites parallèles à l’axe des pressions.

Grandeurs thermodynamiques relatives aux gaz parfaits

Pour un fluide quelconque, il est commode de considérer S, V, T, P comme des variables thermodynamiques et les grandeurs U, F, G, H comme des fonctions dépendant de ces variables. En fait, les variables S, V, T, P sont surabondantes pour décrire l’état d’un fluide en équilibre: si l’on suppose par exemple T et V connus, P s’en déduit par l’équation d’état et S peut se calculer à partir des données moléculaires par les méthodes de la mécanique statistique. Autrement dit, les propriétés particulières du fluide considéré sont définies par les deux lois physiques:

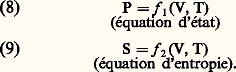La deuxième de ces relations peut être remplacée, pour un corps dont on connaît l’équation d’état, par la connaissance des deux capacités thermiques, à volume constant ou à pression constante:

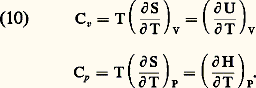Les méthodes de la mécanique statistique permettent de calculer l’énergie libre F d’un système macroscopique à partir des niveaux d’énergie quantifiés occupés par ses constituants et d’en déduire les valeurs des autres fonctions U, G et H. Dans le cas des gaz parfaits, les calculs se simplifient: l’énergie du système est alors la somme des énergies individuelles des molécules (énergie cinétique de translation + énergie d’excitation) et l’on obtient:

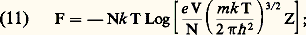e est la base des logarithmes népériens et Z «la somme des états»:

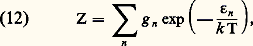﨎ⁿ est l’énergie, et gⁿ la dégénérescence du niveau d’excitation n des molécules. Le calcul de la somme Z dépend des propriétés de la suite des niveaux n et conduit, par exemple, à quelques différences entre les propriétés des gaz monoatomiques ou diatomiques. Cependant, la forme même de l’équation (11) permet d’obtenir quelques résultats généraux valables pour tous les gaz parfaits; on peut en effet la récrire sous la forme:

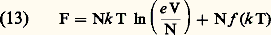où f est une fonction de k T dépendant des propriétés des molécules du gaz. On en déduit par des calculs simples:

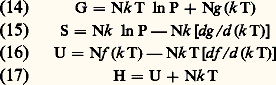avec: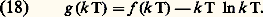

Les équations (16) et (17) permettent d’énoncer des résultats très importants:

– l’énergie interne d’un gaz parfait ne dépend que de sa température (le fait que U soit indépendant de V est d’ailleurs visiblement dû au fait que les interactions entre molécules sont négligeables);

– les capacités thermiques C^v et C^p ne dépendent que de la température;

– la différence entre les deux capacités thermiques est une constante; si l’on désigne par c ^v et c ^p les capacités thermiques rapportées à une molécule et par C^v et C^p les valeurs rapportées à une mole, on a:

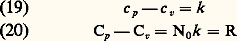(les capacités thermiques étant mesurées ici, comme dans toutes les formules de cet article, en unités d’énergie).

Gaz monoatomiques

Les gaz monoatomiques les plus courants sont les gaz rares (hélium, néon, argon...) et les vapeurs métalliques (lithium, sodium, potassium, mercure...). Dans tous ces gaz, le premier niveau excité est un niveau d’excitation électronique dont l’énergie est de quelques électrons-volts (de 1,4 eV pour le césium à 19 eV pour l’hélium). Dans ces conditions, et si la température n’est pas trop élevée (inférieure à quelques milliers de degrés), tous les atomes sont dans le niveau fondamental. Dans tous les cas pratiques, ce niveau fondamental est un état de nombre quantique orbital L = 0; mais il peut avoir un spin S égal à zéro (gaz rares, mercure), ou à 1/2 (alcalins). La somme des états Z se réduit alors à Z = 2S + 1 et l’on obtient pour les deux premières fonctions thermodynamiques les expressions suivantes:

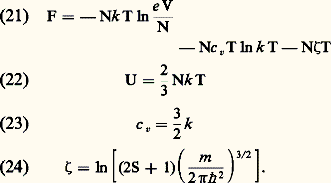La quantité 﨣 est appelée constante chimique.

L’énergie interne d’un gaz parfait mono-atomique est constituée uniquement par l’énergie d’agitation thermique de translation des atomes (relations 22 et 23); la valeur moyenne de celle-ci est égale à 3 k T/2 par atome, soit k T/2 pour chacun des degrés de liberté de translation. Il en résulte que la capacité thermique C^v à volume constant, rapportée à une mole, est constante et égale à 3R/2. Les formules (17) et (19) montrent alors que l’enthalpie d’un tel gaz est 5Nk T/2 et que C^p est également constante et égale à 5R/2.

Gaz diatomiques

Les propriétés thermodynamiques des gaz diatomiques sont compliquées par le fait que les molécules de ces gaz possèdent des énergies de rotation et de vibration qui sont quantifiées, de sorte que l’énergie d’une molécule diatomique peut s’écrire de façon générale sous la forme :

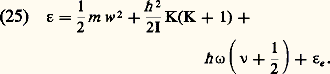Les quatre termes de cette formule sont, dans l’ordre, l’énergie cinétique de translation, l’énergie de rotation, l’énergie de vibration et l’énergie d’excitation électronique de la molécule. Les nombres entiers K et 益 sont les nombres quantiques de rotation et de vibration, I est le moment d’inertie autour d’un axe perpendiculaire à l’axe de la molécule et 諸 est la fréquence de vibration de la molécule. Les valeurs des quanta de rotation 寮²/(2I) et de vibration 寮 諸 ainsi que l’énergie d’excitation 﨎^e du premier niveau électronique sont données pour les principaux gaz dans les tableaux 1, 2 et 3. Les trois termes quantifiés de la formule (25) y sont rangés par ordre d’importance croissante: les quanta de rotation sont de l’ordre de 10^-5 à 10^-2 électronvolts; les quanta de vibration sont de l’ordre de 10^-2 à 0,5 eV; les énergies d’excitation électronique sont de 1 à 10 électronvolts.

Or, de façon générale, on peut associer à toute énergie d’excitation 﨎 une température critique T size=1^﨎, telle que k T size=1^﨎 = 﨎. Dans un gaz en équilibre thermodynamique à une température T 廉 T size=1^﨎, le niveau d’excitation correspondant à T size=1^﨎 est très peu peuplé. Les températures critiques pour les trois modes d’excitation des molécules diatomiques sont les suivantes:

– températures critiques de rotation T^r 黎 10^-1 à 10² kelvins;

– températures critiques de vibration ^v 黎 10² à 5 憐 10³ kelvins;

– températures critiques d’excitation électronique T^e 黎 10⁴ à 10⁵ kelvins.

Les trois températures satisfont aux inégalités:

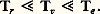Pour tout gaz diatomique, on peut donc distinguer trois domaines de températures.

Premier domaine : T 麗 T^r . Dans ce domaine, les molécules ne possèdent que de l’énergie de translation: l’énergie interne est donnée par la formule (22) des gaz monoatomiques; la capacité thermique C^v est donc, comme pour ceux-ci, égale à 3R/2. Cependant, la constante chimique 﨣 qui intervient dans l’expression de l’entropie est modifiée. En pratique, ce domaine n’est observable que pour l’hydrogène, seul gaz ayant une valeur de T^r effectivement réalisable à l’état gazeux. Dans ce gaz, les calculs sont quelque peu compliqués par l’existence de deux espèces de molécules (orthohydrogène de spin nucléaire total S = 1, parahydrogène de spin nucléaire total S = 0) ^{[cf. HYDROGÈNE]}.

Deuxième domaine : T^r 麗 T 麗 ^v. Lorsque T est de l’ordre de T^r , les premiers niveaux de rotation commencent à se peupler. L’énergie interne croît alors plus vite que (3/2) Nk T du fait de l’énergie d’excitation des rotations. Lorsque l’inégalité T 礪 T^r est devenue forte, de très nombreux niveaux de rotation sont peuplés; on montre alors qu’un calcul classique de l’énergie de rotation est possible et que chacun des deux degrés de liberté de rotation des molécules possède une énergie moyenne égale à k T/2. Cependant, aussi longtemps que l’on a T 廉 ^v, toutes les molécules restent sur le niveau fondamental de vibration; l’énergie interne ne contient que les composantes de translation et de rotation et l’on a:

avec pour les molécules les plus courantes (spin S et moment cinétique orbital L = 0):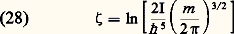

Troisième domaine:^v 麗 T 麗 T^e . Lorsqu’on franchit la région T 黎 ^v, c’est au tour des vibrations des molécules d’être excitées. Il en résulte à nouveau une variation de c ^v; la contribution des vibrations à c ^v est donnée par la formule générale:

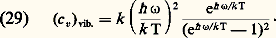On vérifie facilement sur cette formule que (c ^v) ^vib. 轢 k lorsque 寮 諸 拾 k T. Autrement dit, lorsque T 拾 ^v, les vibrations des molécules apportent une contribution à l’énergie interne égale à 2 憐 (k T/2). (On peut considérer que cela correspond à k T/2 pour l’énergie cinétique et k T/2 pour l’énergie potentielle.) Aussi longtemps que T reste nettement inférieur à T^e , on observe donc un nouveau palier sur lequel on a:

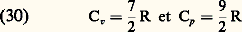avec (en supposant toujours S = L = 0):

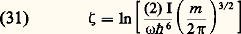le facteur (2) devant être omis dans les molécules constituées d’atomes identiques.

Un calcul plus détaillé, tenant compte du caractère anharmonique des oscillations de grande amplitude des molécules, indique qu’il faut ajouter à c ^v une petite contribution proportionnelle à T.

La figure 3 montre les valeurs expérimentales de la chaleur C^p dans l’hydrogène et illustre la discussion précédente. Les paliers C^p = (5/2) R et C^p = (7/2) R apparaissent nettement; le palier de vibration (C^p = (9/2) R) n’est pas atteint. Il serait atteint (courbe en tireté) si on considérait la capacité thermique à composition chimique constante.

Dans la région au-dessus de 2 000 kelvins, l’hydrogène commence à se dissocier selon la réaction H²2H. Cette dissociation consomme de l’énergie et, dans la région comprise entre 3 000 et 5 000 kelvins, C^p présente un maximum dû à cette réaction. Vers 6 000 kelvins la dissociation est complète, le gaz est redevenu monoatomique et ne possède plus que son énergie de translation; on observe alors un palier entre 6 000 et 8 000 kelvins, avec C^p = 2(5/2) R (le facteur 2 est dû au fait que dans une mole il y a maintenant 2⁰ atomes libres). Si on augmente encore T, les atomes d’hydrogène commencent à s’ioniser vers 8 000 kelvins selon la réaction HH⁺ + e ; entre 10 000 et 20 000 kelvins apparaît un nouveau maximum de C^p , dû à l’énergie consommée par cette réaction. Enfin, aux très hautes températures, le gaz est complètement ionisé et l’on observe un dernier palier, avec C^p = 4(5/2) R (le plasma formé contient maintenant 4⁰ particules libres par mole).

Gaz polyatomiques

Les propriétés de rotation et de vibration des molécules polyatomiques sont plus complexes que celles des molécules diatomiques: une molécule polyatomique possède trois moments d’inertie, en général différents, autour de trois axes d’inertie orthogonaux entre eux; elle possède d’autre part plusieurs modes (en nombre s ) de vibration caractéristiques. Les tableaux 1, 2 et 3 fournissent les ordres de grandeurs des énergies d’excitation des rotations et des vibrations dans quelques gaz polyatomiques. En principe on a alors à haute température des contributions à la capacité thermique c ^v données par:

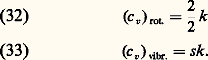Cependant, la dernière contribution n’est presque jamais observée, du fait de la dissociation des molécules.

3. Gaz réels en équilibre thermodynamique

Lorsque la densité d’un gaz n’est pas très faible, les interactions entre molécules ne sont plus négligeables et les propriétés du gaz s’écartent de celles du gaz parfait.

Équation d’état des gaz réels

La figure 4 représente un diagramme d’état des gaz rares, obtenu en portant en abscisse la pression «réduite» P/P^c et en ordonnées la combinaison PV/RT. On a tracé les isothermes, en indiquant sur chacune d’elles la température réduite T/T^c . À l’aide des coordonnées réduites, on représente sur un seul diagramme l’ensemble des résultats relatifs aux cinq gaz rares. Les isothermes de températures T 拾 T^c se confondent pratiquement avec la droite horizontale PV/RT = 1; dans cette région, le gaz obéit assez bien à la loi des gaz parfaits. Aux températures plus basses, le gaz obéit encore à la loi des gaz parfaits aux pressions infiniment faibles. Par contre, aux valeurs non nulles de P, les isothermes à basse température s’écartent d’autant plus de la loi des gaz parfaits qu’on se rapproche du point critique C. Pour représenter ces propriétés des gaz réels, on a utilisé de nombreuses équations d’état; les deux plus importantes sont, d’une part, le développement suivant la puissance de la densité et, d’autre part, l’équation de Van der Waals.

– Développement suivant la puissance de la densité. L’équation d’état ainsi développée s’écrit:

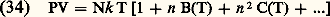Les coefficients B, C sont appelés respectivement deuxième, troisième coefficient du viriel. Ce développement s’appuie sur une base théorique solide: B tient compte des interactions binaires entre particules, C des interactions ternaires; B peut ainsi se calculer de façon générale à partir de la loi du potentiel d’interaction 﨏 entre deux molécules. Dans un gaz monoatomique, 﨏 ne dépend que de la distance r = | る | entre deux atomes et on obtient:

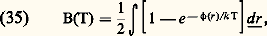où dr 漣 est l’élément de volume associé au vecteur position relative る. On peut généraliser cette formule au cas des gaz polyatomiques.

De la forme de la loi de variation de 﨏 (r ) avec r (cf. théorie CINÉTIQUE DES FLUIDES), on peut déduire que B(T) est positif aux hautes températures et négatif aux basses températures. Ce résultat est bien vérifié expérimentalement, comme on peut le voir sur la figure 4: les isothermes partent de l’axe P = 0 avec une pente qui est positive à haute température et négative à basse température.

– Équation de Van der Waals. C’est une équation semi-empirique qui permet de décrire les gaz dans les régions proches de l’état liquide. Elle fait apparaître le fait que, les liquides étant très peu compressibles, P doit devenir très grand lorsque V tend vers un certain volume limite b , appelé covolume, et elle s’écrit:

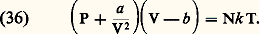On vérifie facilement que le covolume b , le volume critique V^c et le volume «occupé» par les molécules (4/3) N 神r ⁰³ (où r ⁰ est le «rayon» des molécules) sont du même ordre de grandeur. On a par exemple pour les gaz du tableau 1:

Propriétés thermodynamiques des gaz réels

Les interactions entre les molécules font que les diverses fonctions thermodynamiques U, F, G, H et les capacités thermiques C^v et C^p d’un gaz réel diffèrent de celles d’un gaz parfait. Pour chacune de ces grandeurs on peut écrire une équation de la forme: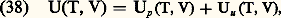

où U^p désigne la valeur pour les gaz parfaits et U^u la contribution due aux interactions. Si la pression n’est pas trop élevée, les interactions portant sur plus de deux molécules sont négligeables et l’on peut calculer les termes d’interaction à partir du deuxième coefficient du viriel B(T) par les formules:

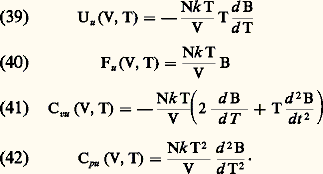L’énergie interne et les chaleurs spécifiques d’un gaz réel ne dépendent donc plus uniquement de la température, comme dans le cas des gaz parfaits, mais aussi de V (ou de P, compte tenu de l’équation d’état).

Aux fortes densités, c’est-à-dire lorsqu’on s’approche de l’état liquide, les interactions d’ordre supérieur deviennent importantes, les formules (39) à (42) ne sont plus valables et les variations avec P des grandeurs U, C^p et C^v sont beaucoup plus importantes. La figure 5 donne par exemple les valeurs de C^p et C^v pour l’argon à P = 0 et à P = 100 atmosphères. On remarque que les effets de gaz réels pour P = 100 atmosphères sont plus importants pour C^p que pour C^v. On peut d’ailleurs montrer qu’au point critique, C^p est infini alors que C^v prend une valeur assez élevée mais finie (environ 15 R pour le xénon).

4. Hydrodynamique et phénomènes de transport

Lorsqu’un gaz n’est pas en équilibre thermodynamique, les écarts qu’il présente par rapport à cet équilibre peuvent avoir des causes très diverses: déséquilibres chimiques dans un mélange en réaction, fonctions de distribution des vitesses très différentes de la loi maxwellienne, hétérogénéités spatiales et mouvements d’ensemble hydrodynamiques. Dans ce paragraphe, on se contentera d’étudier cette dernière famille en considérant un gaz pur, chimiquement inerte, dont l’état local peut être caractérisé par les variables macroscopiques suivantes: densité n , vitesse de fluide ぴ, tenseur de pression 切, vecteur flux de chaleur り. Chacune de ces variables peut dépendre de la position る et du temps t et leur évolution est décrite par les trois équations de transport des particules, de la quantité de mouvement et de l’énergie soit:

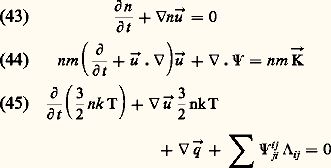où な est la force extérieure par unité de masse, 3 nk T la trace du tenseur 切 et 炙 le tenseur défini en coordonnées cartésiennes (x ¹, x ², x ³) par:

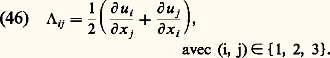Enfin, on a posé:

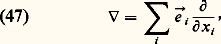les まⁱ étant les vecteurs de base du repère.

Le système des équations (43), (44) et (45) ne constitue pas a priori un système fermé (cf. théorie CINÉTIQUE DES FLUIDES). On peut toutefois le fermer et le résoudre dans le cadre de certaines approximations qui constituent les bases de la mécanique macroscopique des fluides:

– l’approximation d’Euler est la plus grossière; elle consiste à supposer que le fluide est un gaz non visqueux dans lequel la pression 切 se réduit au scalaire P = nk T et que le flux de chaleur り y est nul; on obtient alors les deux équations:

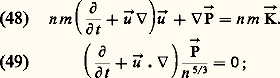la dernière de ces équations exprime le fait que l’écoulement du gaz est adiabatique avec un rapport d’adiabaticité 塚 = 5/3;

– l’approximation de Navier-Stokes peut s’obtenir à partir de la théorie cinétique en poussant les calculs de perturbation un ordre plus loin que dans l’approximation d’Euler; on trouve alors que le tenseur de pression peut se mettre sous la forme:

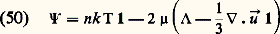où 猪 représente le coefficient de viscosité du gaz.

Le flux de chaleur り

est proportionnel au gradient de température; le coefficient de proportionnalité est la conductivité thermique du gaz.

En reportant dans les équations (43) à (45) les expressions (50) et (51) de 切 et り, on obtient un système fermé.

Les coefficients de conductivité thermique et de viscosité 猪 sont appelés des coefficients de transport; ce sont des caractéristiques du gaz considéré qui peuvent se calculer à partir des sections efficaces de collision entre les molécules du gaz. Ils dépendent en général de la densité et de la température, mais pour un gaz parfait ils ne dépendent que de T.

5. Propriétés physiques moléculaires des gaz

De nombreuses propriétés physiques des gaz se déduisent simplement des propriétés élémentaires des molécules qui les constituent.

Propriétés électriques et optiques

En général, les molécules d’un gaz ne possèdent aucun moment dipolaire dans leur état fondamental. Cependant, si on leur applique un champ électrique つ continu, chaque molécule se polarise et acquiert un moment dipolaire élémentaire 見 つ. La constante de proportionnalité 見 est la polarisabilité des molécules. Les tableaux 1 et 3 indiquent les valeurs de cette grandeur pour les gaz les plus courants. La quantité n 見 est la polarisabilité macroscopique et la permittivité 﨎 du gaz s’en déduit par la formule: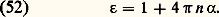

En pratique, il est facile de voir que 﨎 reste très voisin de l’unité. Si le champ électrique appliqué n’est pas un champ continu mais un champ alternatif de fréquence 益, la formule (52) est inchangée à ceci près que 見 et 﨎 doivent maintenant en général être considérés comme des fonctions de 益. L’indice de réfraction optique du gaz n ( 益) se déduit de 﨎 par la formule:

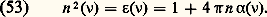En général, si la fréquence 益 est telle que h 益 soit très inférieur aux énergies d’excitation électronique, 見( 益) se confond avec la polarisabilité 見 dans les champs continus, et, dans ce domaine, qui couvre en général tout le spectre infrarouge, les gaz ne présentent pas de propriétés dispersives: l’indice n reste constant et très voisin de l’unité. Dans le domaine visible et ultra-violet, la situation se complique; 見 ( 益) varie notablement: le milieu devient dispersif; de plus 見 ( 益) et 﨎 ( 益) peuvent alors être complexes et le gaz présente des raies et des bandes d’absorption.

Les molécules de certains gaz possèdent une certaine dissymétrie qui leur donne dans leur niveau fondamental un moment dipolaire électrique en l’absence de tout champ appliqué. La dernière colonne du tableau 3 permet d’établir la liste des principaux gaz «dipolaires» avec la valeur du moment électrique dipolaire ら de leurs molécules. Dans un gaz dipolaire qui n’est soumis à aucun champ électrique, les moments dipolaires moléculaires sont orientés de façon aléatoire dans toutes les directions et le moment dipolaire électrique macroscopique は est nul. Par contre, si l’on applique un champ électrique つ continu, celui-ci tend à orienter dans son sens tous les moments dipolaires élémentaires et il apparaît pour les champs électriques faibles un moment macroscopique は proportionnel à つ. Les propriétés de polarisation des gaz dipolaires dans un champ électrique sont analogues à celles des gaz paramagnétiques dans un champ magnétique ^{[cf. MAGNÉTISME]}; en particulier on prévoit dans un champ très élevé (lorsque p E 礪 k T) une saturation de P à la valeur Np. Mais, compte tenu des ordres de grandeur de p , cette saturation ne peut pas s’observer et l’on reste toujours dans le domaine linéaire où つ est proportionnel à は.

Enfin, si l’on applique un champ alternatif dans un gaz dipolaire, les effets de dispersion se produiront à des fréquences assez basses, car la polarisation d’un gaz dipolaire implique une rotation des molécules, phénomène relativement lent.

Propriétés magnétiques

La plupart des molécules gazeuses ne possèdent aucun moment magnétique dans leur niveau fondamental. L’application d’un champ magnétique で dans un tel gaz induit cependant dans chaque molécule un moment magnétique élémentaire proportionnel et de sens inverse à で. La plupart des gaz sont donc diamagnétiques.

Dans quelques gaz, les molécules présentent dans leur niveau fondamental un moment magnétique ゆ. Sous l’action d’un champ magnétique, ces moments ゆ sont orientés et de tels gaz, appelés paramagnétiques, possèdent une susceptibilité magnétique relativement importante, positive, et inversement proportionnelle à T. Théoriquement, le moment magnétique macroscopique se sature dans les champs très forts (lorsque m H 礪 k T) à la valeur Nm mais cette saturation est difficile à observer.

6. Décharges électriques dans les gaz

Si le champ électrique appliqué à un gaz est suffisamment intense, celui-ci devient plus ou moins conducteur et les phénomènes complexes qui se produisent alors portent le nom de décharges dans les gaz: ils sont dus à l’apparition d’électrons et d’ions libres.

Décharges en courant continu à basse pression

Un tube à décharge classique est constitué d’un tube de verre de quelques centimètres de diamètre, muni à ses deux extrémités de deux électrodes planes (distantes de d ) et rempli d’un gaz sous une pression de l’ordre de 1 hectopascal. Au moyen du circuit représenté sur la figure 6 on peut appliquer entre les deux électrodes une différence de potentiel continue V. Si V est assez élevée, on observe un courant i dans le tube qui devient d’ailleurs plus ou moins lumineux. En agissant sur la f.e.m. V⁰ du générateur et sur la résistance de charge R on peut faire varier i depuis des valeurs très faibles, de l’ordre de 10^-18 ampères, jusqu’à des valeurs de quelques dizaines d’ampères. À chacune des valeurs de i correspond une valeur de V; la courbe obtenue en portant i en abscisse et V en ordonnée est appelée la caractéristique (i , V) du tube; la figure 7 représente une telle caractéristique (en coordonnées logarithmiques pour i ); elle fait apparaître divers régimes de décharges que nous allons décrire succinctement.

Décharges non autonomes

Aux courants très faibles, la décharge ne se produit que s’il existe une source extérieure produisant des charges électriques dans le gaz. Si la cathode est dans l’obscurité, l’agent d’ionisation extérieur est constitué par les rayons cosmiques (fig. 7, branche A B). Si la cathode est éclairée par de la lumière contenant des rayons ultra-violets, les courants obtenus sont plus intenses (fig. 7, branche A B) et croissent avec l’éclairement de la cathode. Ils sont dus à l’émission photoélectrique de la cathode. Dans les deux cas, si l’on supprime l’action de l’agent extérieur (blindage du tube, arrêt de l’éclairement), on constate que le courant disparaît; la décharge ne s’entretient pas par elle-même: on dit qu’elle est non autonome.

Décharge sombre de Townsend

Quand on s’approche du point B, de petites variations de V correspondent à des accroissements très importants de i ; dans cette région on montre que le courant est de la forme:

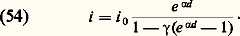Dans cette formule, i ⁰ représente le courant dû aux sources extérieures, le facteur e size=1^見d décrit un effet de multiplication des électrons dans le gaz par les collisions ionisantes électron-molécule, le facteur 塚 décrit divers effets secondaires de production de nouveaux électrons (par exemple, émission d’électrons secondaires due au bombardement de la cathode par les ions produits dans le gaz).

Les coefficients 見 et 塚 (coefficients de Townsend) décrivent un cycle de deux réactions en chaîne. Lorsque le rendement de ce cycle est égal à l’unité, le dénominateur de la formule (54) s’annule (condition de claquage), la décharge devient autonome et le courant n’est plus limité que par le circuit extérieur. La valeur V^d correspondante du potentiel est le «potentiel disruptif». Tant que l’on n’atteint pas le point C (fig. 7), les densités électroniques restent toutefois relativement faibles; il en résulte que les phénomènes de charge d’espace sont négligeables et que la luminosité du gaz reste faible (décharge sombre de Townsend).

Pour un gaz et une cathode donnés, le potentiel disruptif V^d est une fonction du produit Pd (loi de Paschen), où P est la pression et d la distance interélectrode. Pour une certaine valeur optimale (Pd )^m de ce produit, le potentiel disruptif passe par un minimum V^m (minimum de Paschen). On peut expliquer qualitativement l’existence de ce minimum en disant que, aux faibles valeurs de Pd , il n’y a pas assez de molécules dans le tube pour que l’ionisation soit importante, et que, aux fortes valeurs de Pd , la présence d’un trop grand nombre de molécules empêche les électrons d’atteindre des énergies suffisantes pour produire l’ionisation. Les valeurs de V^m et (Pd )^m dépendent du gaz et de la nature de la cathode employée. Le tableau 4 fournit quelques résultats typiques.

Décharges luminescentes

Si l’on augmente encore le courant, on constate que le tube devient assez lumineux et que le potentiel V décroît. La luminosité n’est pas homogène: le tube présente une suite caractéristique de régions lumineuses et sombres. Cela tient au fait que les effets de charge d’espace sont maintenant importants: le champ électrique entre les électrodes n’est plus uniforme; il est concentré au voisinage de la cathode; ce réarrangement du champ le rend plus efficace pour l’ionisation, d’où la diminution de V.

Après les régions de transition C D E, on atteint le palier E F, qui correspond à la décharge luminescente dite normale . Les décharges luminescentes trouvent de nombreuses applications, notamment dans l’éclairagisme (tubes à néon, tubes fluorescents). Leurs propriétés sont assez bien connues; elles sont résumées sur la figure 8 qui montre la répartition, le long du tube, de la brillance, du potentiel V, des densités électroniques et ioniques n ^e et n ⁱ et des densités de courants correspondantes j ^e et j ⁱ . La chute de potentiel et l’entretien de la décharge se produisent principalement dans la région cathodique, qui est caractérisée par les paramètres V ⁿ (chute de potentiel cathodique normale) et d ⁿ (longueur de l’espace cathodique normal). On montre que tout au long du palier E F (fig. 7) de la décharge normale, les grandeurs V ⁿ et d ⁿ restent constantes, mais que la décharge n’occupe qu’une partie de la surface de la cathode avec une densité de courant j ⁿ constante sur la partie utile de la cathode. Les grandeurs V ⁿ , Pd ⁿ et j ⁿ /P² sont caractéristiques du couple gaz-métal de cathode que l’on utilise. Le tableau 4 fournit quelques résultats typiques. V ⁿ est légèrement inférieur au minimum de Paschen, de l’ordre de 0,7 V ^m .

Régime d’arc

Si l’on augmente suffisamment i dans une décharge luminescente normale, toute la surface de la cathode est utilisée et on pénètre avec l’arc F G (fig. 7) dans le régime de décharge luminescente anormale caractérisé par une augmentation rapide de V.

Si l’on augmente encore le courant, V recommence à décroître et, après une région de transition, on atteint le régime d’arc. Ce régime peut prendre des formes diverses, mais il est toujours caractérisé par l’apparition d’effets thermiques importants: le gaz est fortement chauffé, les électrodes également, la cathode peut émettre des électrons par effet thermoionique. La tension V devient très basse (quelques dizaines de volts) et le courant n’est en général limité que par la résistance de charge. Un tube fonctionnant en régime d’arc devra être en général robuste et sérieusement refroidi; l’apparition accidentelle d’un régime d’arc dans un tube non spécialement étudié pour ce régime conduit en général à la destruction du tube.

Décharges en courant continu à haute pression

Lorsque dans un tube à décharge le produit Pd est supérieur à 666 Pa.m, les propriétés des décharges sont profondément modifiées. Les modifications portent essentiellement sur le régime de Townsend et sur la décharge luminescente, tandis que les arcs à haute pression ne diffèrent pas essentiellement des arcs à basse pression. Enfin, dans de nombreux cas, on voit apparaître les décharges filamentaires appelées étincelles: il s’agit de régimes essentiellement transitoires qui conduisent à l’amorçage d’un arc si le générateur est assez puissant. Les décharges à haute pression sont moins bien connues que les décharges à basse pression, car certains des processus fondamentaux qui s’y produisent se font à une échelle spatiale ou temporelle difficile à observer (gaines cathodiques ayant des épaisseurs de l’ordre du micromètre, constantes de temps de l’ordre de la nanoseconde). On se bornera ici à décrire l’un des mécanismes de développement d’une étincelle à haute pression (P 黎 1 atmosphère) entre deux électrodes planes. Les phénomènes sont représentés schématiquement sur la figure 9. Tout d’abord, un petit nuage sphérique d’électrons se multiplie exponentiellement par collisions ionisantes: c’est l’avalanche primaire (fig. 9 a). Les ions positifs ainsi produits peuvent être considérés comme immobiles et créent une charge d’espace positive. Lorsque celle-ci a atteint une certaine valeur critique, apparaissent des avalanches secondaires (fig. 9 b) qui sont initiées par un électron produit par photo-ionisation du gaz et qui se dirigent vers la tête de l’avalanche primaire. Du fait de la jonction des avalanches primaires et secondaires, il se forme deux dards de plasma (dards ou streamers ) qui se propagent l’un vers la cathode et l’autre vers l’anode. Lorsqu’ils ont atteint les électrodes, ces dernières sont reliées par un filament de plasma (fig. 9 c) qui forme un arc si le générateur est assez puissant.

Décharges en haute fréquence et claquages laser

Au moyen de l’un des dispositifs représentés sur la figure 10, on peut appliquer un champ électrique HF à un gaz et produire dans celui-ci une décharge sans qu’aucune électrode ne soit en contact avec lui. On peut analyser les propriétés de ces décharges HF, sur un diagramme de coordonnées P et P 炙 ( est la longueur d’onde du champ HF, 炙 la longueur «de diffusion», qui est de l’ordre de la plus petite dimension du récipient). En portant sur un troisième axe le «potentiel» disruptif (E 炙)^d on obtiendrait une surface qui représente la généralisation de la loi de Paschen. L’étude de cette surface montre que l’on peut faire apparaître plusieurs régimes de décharge dans le plan (P, P 炙) (fig. 11). Au centre du diagramme apparaît le régime contrôlé par diffusion qui est fondé sur les mécanismes suivants: le champ HF chauffe les quelques électrons primaires contenus dans le gaz; les électrons se multiplient par collisions ionisantes sur les molécules; les particules chargées se perdent uniquement par diffusion et recombinaison sur les parois.

Ce régime se distingue des régimes BF et continus (contrôlés par mobilité), dans lesquels le champ électrique draine les particules vers les électrodes. De fait, les décharges HF sont plus efficaces que les décharges BF ou continues car E 炙 y est plus faible. On peut enfin noter que, sur la figure 11, le segment AB correspond à une vallée de potentiel disruptif en ce sens que (E 炙)^d y est minimal.

Lorsqu’on focalise dans une enceinte contenant du gaz sous pression le faisceau d’un laser pulsé, on observe, si le flux lumineux au foyer est assez grand (de l’ordre de 10⁵ W/m²), la formation d’une boule de plasma dans cette région focale. De telles décharges par laser s’apparentent aux décharges HF dont elles sont en quelque sorte l’extrapolation vers les fréquences optiques. Elles en diffèrent par les points suivants: les pressions optimales sont très élevées (10⁴ à 10⁵ kilopascals); les premiers électrons sont produits par l’onde lumineuse elle-même, probablement par effet multiphotonique selon la réaction: (h 益)ⁿ + A 轢 e + A⁺; le volume focal est chauffé, en fin de décharge, à des températures très élevées (10⁴ à 10⁵ K). On cherche à réaliser ainsi des plasmas suffisamment denses et chauds dans lesquels se produisent des réactions thermonucléaires. En fait, pour obtenir les températures et les densités nécessaires (face=F0019 黎 10⁷K, quelques milliers de kg . m^-3), ce sont des solides qu’on irradie au laser, de préférence aux gaz à haute pression.

Encyclopédie Universelle. 2012.